
Algorithmic justice in learning models refers to the application of ethical and fairness principles in the development and use of machine learning algorithms. These algorithms are used to make predictions or decisions based on data, and can have a significant impact on people's lives, for example, in the field of job candidate selection, loan approval, assessment of the risk of committing crimes, among others. Algorithmic justice seeks to avoid discrimination and bias in data-driven decision making. However, there are multiple definitions and perspectives on what algorithmic justice means and how it can be achieved. These definitions can be so heterogeneous that it may be impossible to obtain two or more of these simultaneously in a single estimate. In this blog, based on the article On Fairness and Calibration [1] two different definitions of algorithmic fairness are explained and a graphical demonstration of the impossibility of achieving both is given.
Concepts of fairness
Two definitions of fairness are considered: Equalized Odds and Calibration. For this, we define a classifier h that takes values between 0 and 1, a protected variable A with two possible values 1 and 2 (e.g. female or male sex), and as the actual or observed value of the classification. The classifiers are defined![]() as the constraints of the initial classifier with respect to the two possible values of A. In addition, the values of generalized false positive rate
as the constraints of the initial classifier with respect to the two possible values of A. In addition, the values of generalized false positive rate![]() and generalized true positive rate
and generalized true positive rate ![]() are defined as:
are defined as:
![]()
With this it is possible to define Equalized Odds: a classifier satisfies Equalized Odds if.
![]()
On the other hand, it is possible to state that a classifier is perfectly calibrated if for every value ![]() . Moreover, it satisfies the concept of fairness by calibration if the classifier's restrictions on the categories of the protected variable are also perfectly calibrated. That is,
. Moreover, it satisfies the concept of fairness by calibration if the classifier's restrictions on the categories of the protected variable are also perfectly calibrated. That is,
![]()
Proof of impossibility
In the articles On Fairness and Calibration [1] y Inherent trade-offs in the fair determination of risk scores [2] the impossibility of having both definitions of algorithmic fairness on classifiers ![]() . For this, the geometric implications of both concepts of fairness are initially observed.
. For this, the geometric implications of both concepts of fairness are initially observed.
Given a classifier h, it is possible to represent the performance of the model in a plane as a tuple![]() . If one has two classifiers
. If one has two classifiers ![]() with the same value for the generalized false positive rate, it means that the points in this space must lie on the same vertical line as shown in Figure 1. On the other hand, if
with the same value for the generalized false positive rate, it means that the points in this space must lie on the same vertical line as shown in Figure 1. On the other hand, if ![]() they have the same value for the generalized true positive rate, then the points must lie on the same horizontal line, as shown in Figure 2.
they have the same value for the generalized true positive rate, then the points must lie on the same horizontal line, as shown in Figure 2.
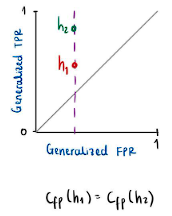
Figure 1
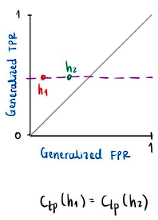
Figure 2
Therefore, to have Equalized Odds both points obtained must coincide, that is to say that
![]()
Now, a perfectly calibrated classifier can be represented by a calibration curve as shown in Figure 3. In this curve, the observations X are separated into different sets or bins depending on the probability assigned to the observation with the classifier h. For example, if we consider all the observations assigned a probability of 0.1, we have that ![]()
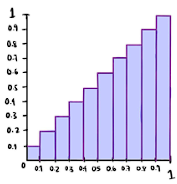
Figure 3
By the definition of a perfectly calibrated classifier we have that for any value p ∈ [0,1]:
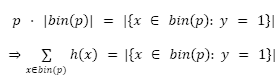
Where |C| represents the cardinality of the set C.
If this result is used on all the values taken from p
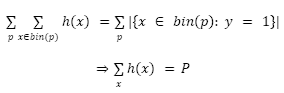
From this, it is possible to obtain the following equality
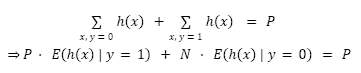
Taking ![]() , one has that for a perfectly calibrated classifier,
, one has that for a perfectly calibrated classifier,
![]()
That is to say that there is a linear relationship between the values of ![]() and
and ![]() . If we now have two perfectly calibrated
. If we now have two perfectly calibrated![]() classifiers with respective values of
classifiers with respective values of ![]() , the points obtained in the plane must lie on the respective straight lines defined by the equation obtained. Figure 4 shows the straight lines on which the tuples must be found for
, the points obtained in the plane must lie on the respective straight lines defined by the equation obtained. Figure 4 shows the straight lines on which the tuples must be found for ![]() respectively.
respectively.
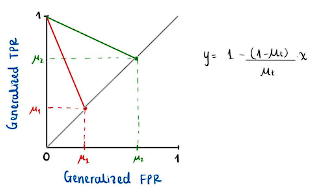
Figure 4
If, in addition to requesting the calibration of both classifiers, we want ![]() them to satisfy Equalized Odds, the points must coincide, so they must be at a point where the two straight lines intersect. If
them to satisfy Equalized Odds, the points must coincide, so they must be at a point where the two straight lines intersect. If ![]() then the only point that satisfies both conditions is the point of intersection of both straight lines, which is the tuple (0,1), which represents the perfect classifier. This concludes the proof of impossibility.
then the only point that satisfies both conditions is the point of intersection of both straight lines, which is the tuple (0,1), which represents the perfect classifier. This concludes the proof of impossibility.
References
[1] G. Pleiss, M. Raghavan, F. Wu, J. Kleinberg, K. Q. Weinberger. On Fairness and Calibration. arXiv:1709.02012, 2017.
[2] J. Kleinberg, S. Mullainathan, and M. Raghavan. Inherent trade-offs in the fair determination of risk scores. In Innovations in Theoretical Computer Science. ACM, 2017.
Get information about Data Science, Artificial Intelligence, Machine Learning and more.
In the Blog articles, you will find the latest news, publications, studies and articles of current interest.