Machine learning models have become essential tools for decision-making in critical sectors such as healthcare, public policy, and finance. However, their practical application faces two major challenges: selection bias in the data and the proper quantification of uncertainty. Without addressing these issues, predictions can be inaccurate, policies unfair, and decisions inefficient. Recent research, such as that presented by Cortes-Gomez et al. (2023, 2024) in their articles Statistical inference under constrained selection bias and Decision-focused uncertainty quantification, was featured in the Quantil seminar as part of the presentation of these research works.
Selection bias arises when the data available to train a model does not faithfully represent the target population, leading to distorted inferences. Formally, the problem can be described as estimating a quantity of interest f(P) over an unknown distribution P, when only data from a potentially biased observed distribution Q is available. In general, P and Q are related by a bias factor (X) = p(X)/q(X), but this ratio is unknown. The proposed solution imposes constraints based on external information—such as census data or serological studies—allowing the definition of a feasible set θ(X), instead of assuming an arbitrary divergence between P and Q, Through an optimization problem, upper and lower bounds on f(P)are obtained, ensuring statistically valid inferences without introducing unverifiable assumptions. These bounds are shown to be asymptotically normal, enabling the construction of robust confidence intervals.
To motivate the need for the proposed methodology, let us first consider a visualization without applying any corrections for selection bias. Figure 1 shows the estimated relative risk of hospitalization due to COVID-19 across different racial groups. However, without a methodology that accounts for selection bias, this graphical representation could be misleading, as it does not allow us to distinguish whether the observed disparities reflect actual inequalities or are merely the result of biases in the observed data. In this context, directly interpreting these differences without proper adjustments could lead to incorrect conclusions.
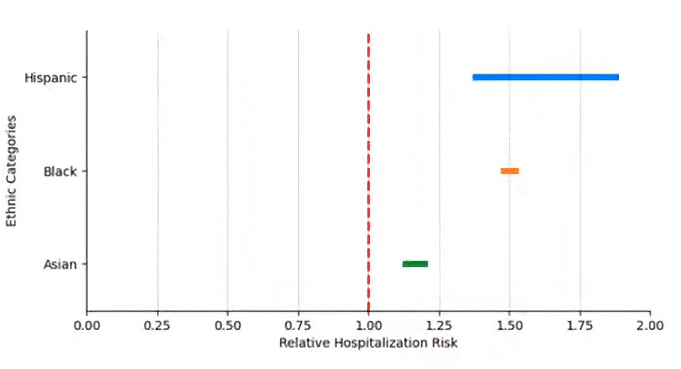
Figure 1. Estimated Relative Risk of Hospitalization Without Correction for Bias
Initially, a graphical representation of the data without correcting for selection bias (as illustrated in Figure 1) may fail to reveal true disparities or even suggest misleading conclusions due to the influence of bias in the observed data. However, by applying the methodology developed by Cortes-Gomez et al. (2023), we obtain Figure 2, which provides statistical guarantees on the validity of the inference. This methodology enables the separation of real disparity effects from those induced by a lack of representativeness in the data, ensuring that the interpretation is accurate and reliable. The results indicate that the proposed method significantly improves the precision of estimates in scenarios where selection bias is a critical issue.
Figure 2 shows the estimated relative risk of hospitalization due to COVID-19 across different racial groups, adjusted using the proposed methodology. According to the results, there is a higher risk of hospitalization among Asian, Black, and Hispanic populations compared to the White population. For the Black and Hispanic groups, the partial identification method used in the study approaches point identification, suggesting strong evidence of structural disparities in hospital access and treatment. Furthermore, the confidence intervals generated in this analysis reflect a significant improvement in estimation precision, enabling robust conclusions without relying on strong assumptions about the underlying distribution.
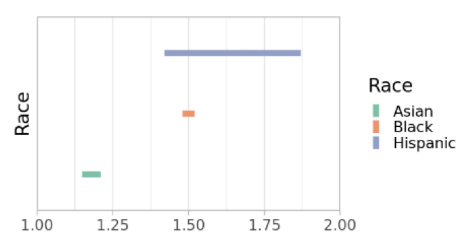
Figure 2. Estimation of f(P) by Racial Group in COVID-19 Hospitalization
Even when bias in the estimates is minimized, uncertainty remains a key challenge. Most current methods for uncertainty quantification produce confidence intervals without taking into account the context in which decisions will be made based on them. In many applications, it is not enough to guarantee that the prediction contains the true value with a certain probability; the prediction sets must also be consistent with the decision-making structure.
Let us consider the example of medical diagnosis in dermatology, as discussed in the article by Cortes-Gomez et al. (2024). A standard conformal prediction method might generate a set of possible diagnoses with a high probability of including the true condition. However, this set could be clinically difficult to interpret if it includes diseases spanning multiple distinct categories—some benign and others malignant. As mentioned in the presentation, different labels within the prediction set imply completely different diagnostic and treatment actions.
To address this limitation, a decision-focused uncertainty quantification approach has been developed. This adapts the conformal prediction framework to minimize a decision loss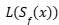 
associated with the prediction set 
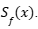The objective is to minimize the 
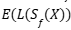expected loss subject to the 
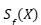constraint that Y the prediction set covers 
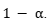. For the case in which the loss function is separable, the problem has a closed-form solution using a Neyman-Pearson–type decision rule, based on the ratio between the conditional probability and the penalty of including each label. In the general case, it is solved through a combinatorial optimization over the prediction set, followed by a conformal adjustment to ensure statistical coverage.
Empirical results show that this approach significantly reduces decision loss compared to standard conformal methods, while maintaining statistical validity. In medical applications, the prediction sets obtained with this method exhibit greater clinical coherence, grouping diagnoses according to their therapeutic similarity and avoiding redundant or contradictory sets. As observed, decision-adjusted prediction sets reduce ambiguity in clinical interpretation, enhancing the usefulness of models in high-uncertainty contexts. This allows physicians to work with sets of possible diagnoses that not only carry a statistical guarantee of containing the true condition but are also more relevant and actionable for treatment planning.
These studies highlight the importance of integrating external information and decision structure into statistical inference and machine learning models. Robustness to selection bias and the adaptation of uncertainty to decision-making enable the development of more reliable and useful models in critical scenarios—from public policy design to AI-assisted medical diagnosis—laying the groundwork for more fair, interpretable, and actionable predictive systems.
Get information about Data Science, Artificial Intelligence, Machine Learning and more.
Link to the seminar presentation
https://www.youtube.com/watch?v=8CNPKVwUGtQ&t=3s&ab_channel=QuantilMatem%C3%A1ticasAplicadas
References
In the Blog articles, you will find the latest news, publications, studies and articles of current interest.
