Mirar la distribución, no sólo el promedio
Supongamos que un gobierno implementa una nueva política de salud que busca reducir hospitalizaciones evitables. Una evaluación tradicional podría decirnos que, en promedio, las hospitalizaciones caen un 10\%. Pero esa cifra única esconde preguntas clave: ¿Quiénes se benefician más: los pacientes de mayor riesgo o los de riesgo medio? ¿La política reduce eventos extremos (colas de la distribución) o solo mejora situaciones moderadas? ¿El impacto es similar en distintas regiones o cohortes de adopción?
The Regresión por Cuantiles (QR) responde precisamente a este tipo de preguntas. En lugar de enfocarse en la media condicional de un resultado Y dado X, nos permite estudiar cómo cambia un cuantil dado (por ejemplo, el percentil 25, 50 o 75) cuando se introduce una política. De forma esquemática, la regresión por cuantiles estima, para un percentil, un predictor lineal que aproxima al cuantil condicional. En vez de castigar cuadráticamente los errores (como hace OLS), QR . La función de pérdida a minimizar, en vez de castigar cuadráticamente los errores (como lo hace regresión sobre la media) castiga de forma distinta los residuos positivos y los negativos, de modo que el percentil queda bien centrado
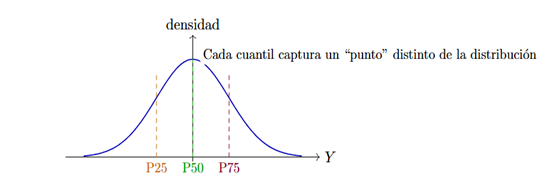
Figura 1: Regresión por cuantiles: mirar cómo se mueve cada cuantil de la distribución, no sólo el promedio.
En evaluación de políticas escalonadas en el tiempo (cuya implementación no es simultanea para todos los beneficiarios) es natural combinar QR con diseños de diferencias en diferencias (DiD). La pregunta es: ¿podemos usar simplemente una regresión por cuantiles con efectos fijos de dos vías (TWFE-QR) y quedarnos tranquilos?
Nuestro trabajo muestra que la respuesta no, y que el problema de comparaciones prohibidas, que ya se conoce en la media, se hereda, de forma sutil, a los cuantiles.
El escenario: políticas con adopción escalonada
Imaginemos un panel con unidades i (municipios, hospitales, empresas) y periodos t (años, trimestres, meses). Cada unidad adopta una política en un momento distinto: algunas temprano, otras tarde, otras nunca. La estimación TWFE-QR busca el valor que mejor ajusta los cuantiles de la distribución de la variable de resultado, una vez absorbidos los efectos fijos. En apariencia, esto es una extensión natural del TWFE clásico al mundo de los cuantiles. Sin embargo, cuando la adopción es escalonada y los efectos de la política difieren entre cohortes, el estimador TWFE-QR termina mezclando comparaciones tratado vs tratado en momentos distintos, algo que va contra la lógica del diseño DiD.
Qué está haciendo realmente TWFE-QR
Detrás de escena, la regresión por cuantiles con efectos fijos resuelve un problema de optimización convexo. Las condiciones de Karush–Kuhn–Tucker (KKT) imponen que, en el óptimo, ciertos balances de residuos deben igualar cero cuando se ponderan por las covariables (incluida la variable de tratamiento). Sin entrar en la notación técnica, el mensaje es que para cada cohorte g (definida por el momento de adopción) y periodo l, podemos pensar en un score asociado a la celda (g,l): mide cuántas observaciones están por encima o por debajo del cuantil objetivo. El estimador TWFE-QR elige un único valor para el estimador del efecto del tratamiento, tal que la suma de todos esos scores, agregados sobre todas las celdas tratadas, se balancee en cero. Si cada cohorte tuviera el mismo efecto de la política, ese balance sería coherente: todas las celdas “empujarían” en la misma dirección. Pero cuando los efectos difieren entre cohortes (heterogeneidad), algunas celdas empujan hacia arriba, otras hacia abajo, y el resultado final es una especie de promedio ponderado de efectos de cohorte.
En nuestro trabajo mostramos que, bajo condiciones generales, TWFE-QR se puede interpretar como un promedio ponderado de los efectos “limpios” de cada cohorte g (si la comparáramos sólo contra controles adecuados), con pesos no negativos que dependen del tamaño de la cohorte, del número de periodos tratados y de cuán informativa es la distribución en torno al cuantil de interés. El problema es que estos pesos no responden explícitamente a una lógica de política, sino que emergen de las KKT. Los pesos dependen de la estructura del panel y de la densidad de la distribución alrededor del cuantil de interés, no de un criterio de diseño explícito. Desde la perspectiva de política pública, esto dificulta la interpretación: ¿qué efecto estamos reportando realmente? ¿Corresponde a un contraste tratado vs nunca tratado, o mezcla comparaciones tratado vs tratado en distintas etapas de adopción?
Nuestra propuesta
Para enfrentar este problema proponemos un estimador alternativo, que se basa en una idea simple: construimos contrastes limpios por cohorte, luego los agregamos con pesos que tengan una interpretación clara. El procedimiento es el siguiente:
La clave es que cada efecto de comparaciones 2×2 se construye evitando comparaciones tratado vs tratado en momentos inadecuados, y que la agregación final respeta la lógica de diseño: más peso a cohortes con mayor número de observaciones tratadas, pero sin permitir que el propio tratado sea su control en otra etapa.
Qué hemos encontrado en simulaciones
Para ilustrar el comportamiento de ambos estimadores, consideramos un experimento de datos simulados donde: el resultado sin tratamiento combina un efecto fijo por unidad, un efecto fijo por tiempo y un choque aleatorio, el efecto de la política es heterogéneo por cohorte: algunas cohortes tienen un impacto mayor en la cola alta, otras en la mediana, etc. Sobre este escenario, comparamos: el estimador TWFE-QR agregado, que estima un único efecto para todo el panel, y el estimador por cohortes con agregación transparente. Los resultados muestran que: TWFE-QR presenta sesgos relevantes en varios cuantiles (P25, P50, P75) cuando los efectos son heterogéneos. En algunos escenarios, el signo del efecto estimado no coincide con el efecto verdadero. Nuestro estimador reduce el sesgo de manera sistemática a lo largo de la distribución: el sesgo porcentual cae de manera importante entre P25 y P75, y el estimador respeta la dirección correcta del efecto en todos los cuantiles.
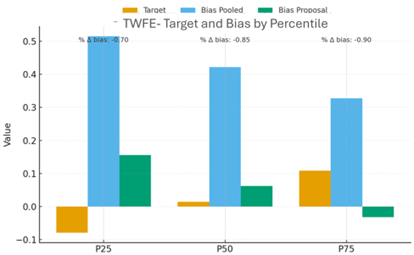
Figura 2: TWFE: objetivo y sesgo a lo largo de los percentiles. En simulaciones con cuatro cohortes (temprana, media, tardía y nunca tratada), el estimador TWFE-QR presenta sesgos importantes y, en algunos cuantiles, puede incluso cambiar de signo frente al efecto verdadero (naranja). Nuestra propuesta (verde) reduce el sesgo de forma consistente en P25, P50 y P75.
Más allá de las métricas numéricas, la interpretación cualitativa también mejora: el analista puede descomponer el efecto en componentes por cohorte, ver qué grupos se benefician más en cada cuantil y comunicar resultados de forma alineada con la realidad de la política (quién se trató cuándo).
Implicaciones
En esta etapa de nuestra investigación, los hallazgos principales han sido: si la política se adopta en distintos momentos y existe sospecha de heterogeneidad de efectos, usar TWFE-QR de forma mecánica lleva a interpretaciones engañosas: el estimador mezcla tratamientos tempranos y tardíos como si fueran controles entre sí. Es necesario, por lo menos, un diseño basado en comparaciones limpias por cohorte para mantener la lógica original de DiD: comparar tratados sólo con “nunca tratados» o “todavía no tratados», y luego construir un promedio que refleje esa estructura. La transparencia de los pesos es crucial: saber exactamente cuánto aporta cada cohorte al efecto agregado facilita la comunicación con tomadores de decisión y el diseño de políticas focalizadas.
Get information about Data Science, Artificial Intelligence, Machine Learning and more.
References
Goodman-Bacon, A. (2021). Difference-in-Differences with Variation in Treatment Timing. Journal of Econometrics, 225(2), 254-277.
Callaway, B., & Sant’Anna, P. H. C. (2021). Difference-in-Differences with Multiple Time Periods. Journal of Econometrics, 225(2), 200-230.
Sun, L., & Abraham, S. (2021). Estimating Dynamic Treatment Effects in Event Studies with Heterogeneous Treatment Effects. Journal of Econometrics, 225(2), 175-199.
In the Blog articles, you will find the latest news, publications, studies and articles of current interest.