
Supongamos que contamos con un modelo de aprendizaje de máquinas, f, que predice el precio de una prima de seguros, Y, para unos datos que incluyen un atributo sensible, como lo es el género. Puede existir una discriminación debido a un sesgo estadístico (injusticias del pasado o desbalance en la muestra), una correlación entre el atributo sensible y alguna variable explicativa, o por un sesgo intencional que se tenga.
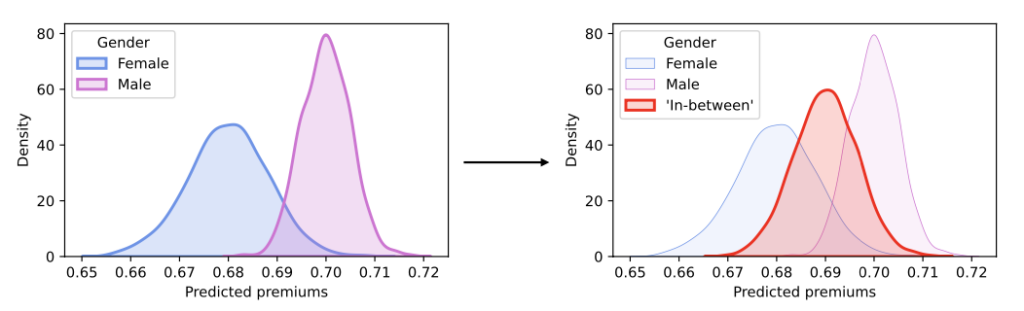
Para evitar este sesgo, ha habido legislaciones (como por ejemplo, AI ACT – Europe, 2024) que limitan, o incluso eliminan, el uso de ciertos atributos sensibles en modelos de inteligencia artificial. Sin embargo, simplemente eliminar estos atributos no es siempre la solución que genera el mejor nivel de justicia ni el mejor rendimiento del modelo. Existen enfoques de preprocesamiento (encargados de modificar los datos de entrada), procesamiento (añaden una penalidad de equidad) y de postprocesamiento (modifican la distribución univariada de las predicciones para crear una distribución intermedia, tal como se hace en Sequential Fairness)
Ha habido varios acercamientos de postprocesamiento para mitigar estos efectos si se tiene un atributo sensible (Single sensitive atribute, SSA). Pero, ¿qué podemos hacer si se cuenta con múltiples atributos sensibles (Multiple sensitive atribute, MSA)? Una posible aproximación es considerar la intersección de las distribuciones creadas por cada una de las combinaciones entre los atributos sensibles. Por ejemplo, si se tiene como atributos sensibles género (femenino y masculino), y origen étnico (negro y blanco), se considerarían estos cuatro casos con el enfoque de SSA:

Esto puede ser costoso computacionalmente entre más atributos sensibles se tengan, además, al añadir un nuevo atributo sensible se pierde el trabajo previamente hecho, porque se deben hallar distribuciones con las nuevas combinaciones. Otra aproximación (que es la que nos atañe en este blog) es la de Sequential Fairness. En resumen, este enfoque busca modificar las predicciones del modelo para que sean justas para el primer atributo sensible y, luego, volver a modificar estas nuevas predicciones para que sean justas para el segundo atributo (y en consecuencia también para el primero), y así sucesivamente. Como beneficios a este acercamiento tenemos que este es un proceso conmutativo (no importa el orden de la secuencia de los atributos para hacer al modelo justo), también es fácil añadir nuevos atributos sensibles y, además, hace más sencilla su interpretabilidad.
La idea es hallar una distribución representativa que se encuentre entre las distribuciones condicionales para las predicciones de los atributos sensibles. Esto se logra usando el baricentro de Wasserstein, intentando minimizar el costo total de mover una distribución a otra mediante el transporte óptimo. El concepto del baricentro de Wasserstein extiende la idea de la paridad demográfica fuerte (Strong Demographic Parity) a múltiples atributos, la cual busca reducir la inequidad en grupos y requiere que las predicciones de un modelo sean independientes de los atributos sensibles.
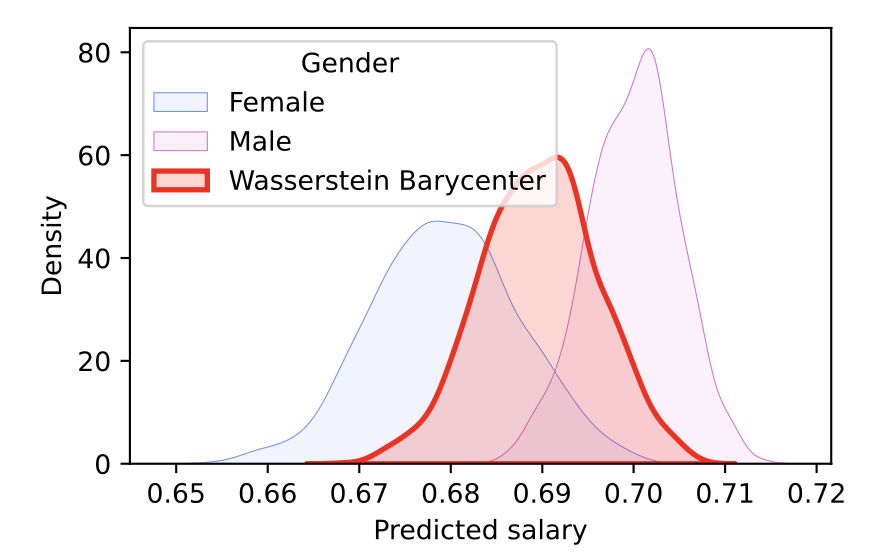
Es importante tener en cuenta que los métodos para reducir la injusticia de los modelos de predicción siempre tienen un costo en el rendimiento. Sin embargo, este acercamiento, al usar el baricentro de Wasserstein, hace que las métricas de accuracy y MSE tengan el menor daño posible.
Equipy es un paquete de Python que implementa Sequential Fairness en las predicciones de modelos de predicción continua de aprendizaje de máquinas que contengan múltiples atributos sensibles, que usa el concepto del baricentro de Wasserstein para no afectar de gran manera el rendimiento del modelo y mitigar el sesgo y la discriminación que puede haber en las predicciones por tener atributos sensibles.
Obtén información sobre Ciencia de datos, Inteligencia Artificial, Machine Learning y más.
En los artículos de Blog, podrás conocer las últimas noticias, publicaciones, estudios y artículos de interés de la actualidad.