
La electricidad es un componente esencial de la sociedad que tiene implicaciones sobre la economía, el medio ambiente y el bienestar de los consumidores. La necesidad de una provisión de energía asequible, segura y limpia nos motiva a seguir mejorando los mercados de electricidad. En Colombia, la generación de energía eléctrica se organiza a partir de subastas donde los generadores ofertan capacidades máximas de generación para cada una de las 24 horas del día siguiente, junto con un precio unitario. El operador del sistema, a partir de una regla de asignación y de pagos, define el número de unidades que va a despachar cada generador y el pago que van a recibir. En este contexto, surge la pregunta de cómo diseñar esta subasta para minimizar los costos de generación del sistema para proveer la demanda de electricidad, incentivando a que los generadores participen en la subasta y revelen sus verdaderos costos unitarios.
Sin embargo, resolver esta pregunta conlleva varios desafíos. En primer lugar, es importante considerar que los generadores poseen información privada sobre sus costos unitarios y actúan de manera estratégica para maximizar sus beneficios, ofertando un precio por encima de sus costos reales. Además, pueden existir otros objetivos además de minimizar los costos de generación, como la reducción del impacto ambiental de la generación térmica y garantizar la seguridad del sistema para satisfacer la demanda. Por ejemplo, la energía hídrica suele ser una fuente de generación costo efectiva en Colombia. No obstante, como hemos observado en el último mes, eventos climáticos extremos como es el fenómeno del Niño pueden provocar aumentos considerables en los precios de energía.
La literatura sobre el diseño óptimo de subastas, comenzando con Myerson (1981), ofrece perspectivas valiosas sobre cómo abordar esta pregunta. Recientemente, Dütting et al. (2019) propone un método para encontrar diseños óptimos de subastas usando Aprendizaje Profundo. Motivada por este contexto, mi trabajo de tesis, titulado Optimal Design for Electricity Auctions: A Deep learning approach tiene como objetivo extender este método para descubrir diseños de subastas de electricidad. En particular, los resultados que se presentarán en este espacio evalúan el impacto de la integración de energía eólica y solar en los costos de generación del sistema, usando datos del mercado colombiano durante el 2022.
El método empleado consiste en primero modelar el problema de diseño de subastas de múltiples unidades para proveer la demanda de electricidad durante diferentes franjas de tiempo a lo largo del día. Se parte del supuesto de que los generadores tienen un único costo unitario privado durante el día, que sigue una distribución de probabilidad conocida. Asimismo, disponen de capacidades para cada franja de tiempo. Por medio de una subasta, los generadores reportan sus costos unitarios y el operador del sistema, define cuantas unidades va a despachar cada generador en cada franja, y el pago que van a recibir por generar estas unidades. Estas reglas de asignación y de pagos se modelan a través de redes neuronales, que se entrenan para resolver el problema de diseño óptimo.
El problema de diseño óptimo se enfoca en encontrar las reglas de asignación y de pagos que minimizan los costos esperados de generación de energía eléctrica y cumplen con 4 restricciones:
Después, se reformula el problema de diseño óptimo como un problema de aprendizaje. Las restricciones de compatibilidad en incentivos y capacidad se relajan de manera que se cumplan en valor esperado. Las otras dos restricciones se incorporan dentro de la arquitectura de la red. La red neuronal se entrena usando muestras aleatorias de los costos unitarios siguiendo su distribución conjunta conocida. El objetivo es minimizar una función de perdida que incorpora tanto los costos de generación como las violaciones a estas restricciones.
A continuación, se presentan los resultados de los experimentos usando datos reales del mercado de electricidad colombiano durante el 2022 para estimar la distribución de los costos unitarios, capacidades y demanda para cada tipo de generador: (1) termoeléctrico que usa combustibles líquidos, (2) termoeléctrico que emplea carbón o gas, (3) hidroeléctrico, (4) eólico y (5) solar. Además, se modela el despacho durante 2 franjas de tiempo, una de baja demanda (entre 10pm-8am) y la otra de alta demanda (9am-9pm). El primer escenario (A), considera únicamente 3 generadores: los dos termoeléctricos y uno hidroeléctrico. A partir de este escenario de referencia los experimentos B-D expanden la capacidad en un 10%, 20% y 30%, respectivamente, incorporando un generador eólico y solar. En contraste, los escenarios E-G incorporan dos generadores hidroeléctricos adicionales para cada nivel de expansión.
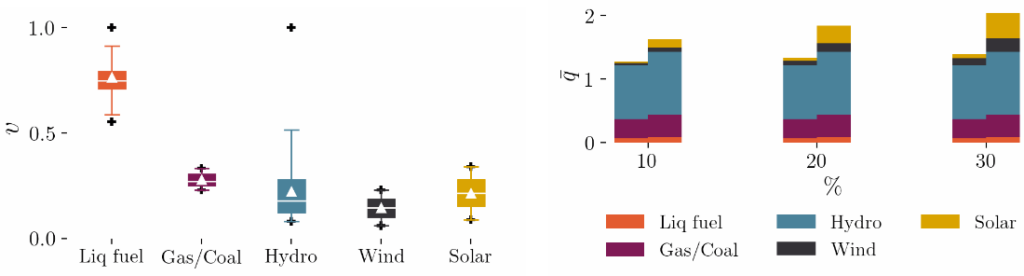
Figura 1: Diagrama de cajas de los costos unitarios para cada generador (lado izquierdo) y capacidad promedio para cada generador (lado derecho) durante cada franja de tiempo para los experimentos B-D. Los triángulos y el signo + representan indican los valores promedios y máx./min., respectivamente. Las barras de la izquierda en la gráfica izquierda representan la capacidad promedio durante la primera franja, mientras que las de la derecha corresponden a la segunda franja.
El lado izquierdo de la Figura 1 muestra la distribución de los costos unitarios para cada generador. Aunque en promedio los generadores hidroeléctricos, eólicos y solares tienen costos unitarios similares, se observa una distribución sesgada a la derecha para el generador hidroeléctrico. Estos costos elevados suelen asociarse con periodos de lluvias reducidas: la generación agota rápidamente los niveles de los embalses cuando hay sequía. Esto conlleva a que los generadores hidroeléctricos presenten mayores costos de oportunidad: si se genera electricidad se sacrifican pagos considerables en el futuro. Por otro lado, para los experimentos B-D, el lado derecho de la Figura 1 muestra la capacidad promedio de cada generador para la primera y segunda franja, a lo largo de cada nivel de expansión de la capacidad agregada. Se evidencia que, en la segunda franja, la capacidad aumenta más, lo cual se debe a la mayor disponibilidad de energía solar.
La Figura 2 compara las distribuciones de los pagos a los generadores y de los costos de generación entre el escenario D y G (una expansión de la capacidad en un 30%) en la subasta aprendida. A pesar de que los costos de generación promedio del sistema solo se reducen en un 5.1%, se puede evidenciar que integrar energía solar y eólica reduce la incidencia de costos extremos de generación a comparación de cuando se añaden nuevos generadores hidroeléctricos. Estos valores extremos usualmente suceden cuando los costos unitarios del generador hidroeléctrico son altos durante periodos de poca lluvia.

Figura 2: Distribución de pagos y costos de generación para un nivel de expansión del 30% para los escenarios D (panel de la izquierda) y G (panel del medio). El histograma de los costos de generación cuando se introduce energía eólica y solar se muestran en negro y cuando se introducen generadores hidroeléctricos adicionales en azul claro.
En general, este trabajo espera proponer un método que permita explorar más aplicaciones para subastas de electricidad. Trabajos futuros pueden incluir restricciones adicionales relacionadas con niveles de contaminación o modelar costos no convexos. Además, se podría estudiar el efecto de programas de respuesta de la demanda y de estrategias de capacidad de reserva.
Referencias:
Myerson, R. B. (1981): “Optimal auction design,” Mathematics of operations research, 6, 58–73.
Dütting, P., Z. Feng, H. Narasimhan, D. Parkes, and S. S. Ravindranath (2019): “Optimal auctions through deep learning,” in International Conference on Machine Learning, PMLR, 1706–1715.
Obtén información sobre Ciencia de datos, Inteligencia Artificial, Machine Learning y más.
En los artículos de Blog, podrás conocer las últimas noticias, publicaciones, estudios y artículos de interés de la actualidad.