Los modelos de aprendizaje automático se han convertido en herramientas esenciales para la toma de decisiones en sectores críticos como la salud, las políticas públicas y las finanzas. Sin embargo, su aplicación práctica enfrenta dos grandes desafíos: el sesgo de selección en los datos y la cuantificación adecuada de la incertidumbre. Sin abordar estos problemas, las predicciones pueden ser erróneas, las políticas injustas y las decisiones ineficientes. Investigaciones recientes, como las presentadas por Cortes-Gomez et al. (2023, 2024) en sus artículos Statistical inference under constrained selection bias y Decision-focused uncertainty quantification, fueron expuestas en el seminario de Quantil como parte de la presentación de estos trabajos de investigación.
El sesgo de selección surge cuando los datos disponibles para entrenar un modelo no reflejan fielmente la población objetivo, generando inferencias distorsionadas. Formalmente, el problema puede describirse como la estimación de una cantidad de interés f(P) sobre una distribución desconocida P, cuando solo se tiene acceso a datos de una distribución observada Q potencialmente sesgada. En general, P y Q están relacionadas por un factor de sesgo (X) = p(X)/q(X), pero este ratio es desconocido. La solución propuesta impone restricciones basadas en información externa, como censos o estudios serológicos, permitiendo definir un conjunto factible θ para θ(X), en lugar de asumir una divergencia arbitraria entre P y Q. Mediante un problema de optimización, se obtienen límites superiores e inferiores sobre f(P), asegurando inferencias estadísticamente válidas sin introducir suposiciones no verificables. Se demuestra que estos límites son asintóticamente normales, permitiendo la construcción de intervalos de confianza robustos.
Para motivar la necesidad de la metodología propuesta, consideremos primero una visualización sin aplicar correcciones al sesgo de selección. La Figura 1 muestra la estimación del riesgo relativo de hospitalización por COVID-19 en diferentes grupos raciales. Sin embargo, sin una metodología que controle el sesgo de selección, esta representación gráfica podría ser engañosa, ya que no permite diferenciar si las disparidades observadas reflejan desigualdades reales o simplemente son el resultado de sesgos en los datos observados. En este contexto, interpretar directamente estas diferencias sin ajustes adecuados podría llevar a conclusiones incorrectas.
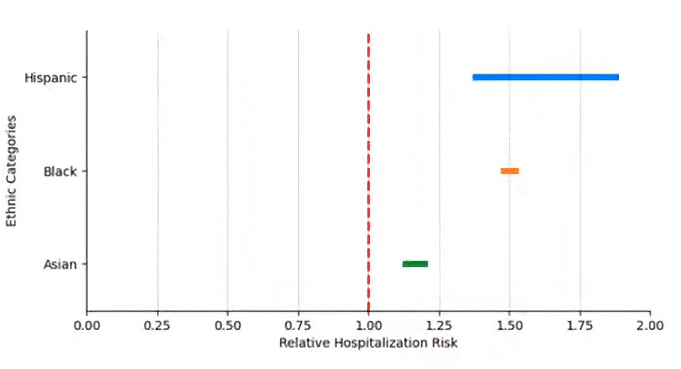
Figura 1. Estimación del Riesgo Relativo de Hospitalización sin Corrección por Sesgo
Inicialmente, una representación gráfica de los datos sin corregir por el sesgo de selección (como se ilustra en la Figura 1) podría no revelar las verdaderas disparidades o incluso sugerir conclusiones erróneas debido a la influencia del sesgo en los datos observados. Sin embargo, al aplicar la metodología desarrollada por Cortes-Gomez et al. (2023), obtenemos la Figura 2, que proporciona garantías estadísticas sobre la validez de la inferencia. Esta metodología permite separar los efectos reales de las disparidades de aquellos inducidos por la falta de representatividad en los datos, asegurando que la interpretación sea correcta y confiable. Los resultados obtenidos indican que el método propuesto mejora significativamente la precisión de las estimaciones en escenarios donde el sesgo de selección es problemático.
La Figura 2 muestra la estimación del riesgo relativo de hospitalización por COVID-19 en diferentes grupos raciales, ajustada por la metodología propuesta. De acuerdo con los resultados obtenidos, se observa un mayor riesgo de hospitalización en las poblaciones asiática, negra e hispana en comparación con la población blanca. Para los grupos negro e hispano, el método de identificación parcial utilizado en el estudio se acerca a una identificación puntual, lo que sugiere una fuerte evidencia de disparidades estructurales en el acceso y tratamiento hospitalario. Además, los intervalos de confianza generados en este análisis reflejan una mejora significativa en la precisión de las estimaciones, lo que permite obtener conclusiones robustas sin depender de supuestos fuertes sobre la distribución subyacente
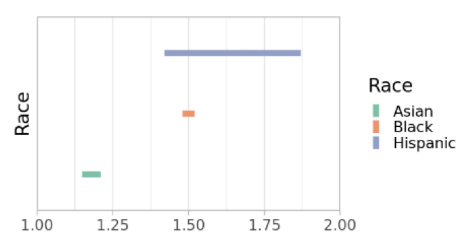
Figura 2. Estimación de f(P) por Grupo Racial en Hospitalización COVID-19
Aun cuando se logra minimizar el sesgo en las estimaciones, la incertidumbre sigue siendo un desafío clave. La mayoría de los métodos actuales de cuantificación de incertidumbre producen intervalos de confianza sin considerar el contexto en el que se tomarán decisiones basadas en ellos. En muchas aplicaciones, no basta con garantizar que la predicción contenga el valor verdadero con cierta probabilidad, sino que los conjuntos de predicción sean coherentes con la estructura de decisión.
Consideremos el ejemplo del diagnóstico médico en dermatología, como se discute en el artículo de Cortes-Gomez et al. (2024). Un método estándar de predicción conformal podría generar un conjunto de posibles diagnósticos con una alta probabilidad de incluir la enfermedad real. Sin embargo, este conjunto podría ser difícil de interpretar clínicamente si incluye enfermedades que abarcan múltiples categorías distintas, algunas benignas y otras malignas. Como se mencionó en la presentación, diferentes etiquetas dentro del conjunto de predicción implican acciones de diagnóstico y tratamiento completamente distintas.
Para abordar esta limitación, se ha desarrollado un enfoque de cuantificación de incertidumbre enfocado en decisiones. Este adapta el marco de predicción conformal para minimizar una pérdida de decisión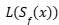 
asociada al conjunto de predicción 
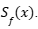Se plantea la minimización de 
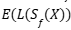bajo la restricción de que 
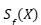cubra la verdadera etiqueta Y con probabilidad al menos 
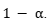Para el caso en que la función de pérdida es separable, el problema tiene solución cerrada mediante una regla de decisión tipo Neyman-Pearson basada en la razón entre la probabilidad condicional y la penalización de incluir cada etiqueta. En el caso general, se resuelve mediante una optimización combinatoria sobre el conjunto de predicción, seguido de un ajuste conformal para garantizar cobertura estadística.
Los resultados empíricos demuestran que este enfoque reduce significativamente la pérdida de decisión en comparación con los métodos conformales estándar, al tiempo que mantiene la validez estadística. En aplicaciones médicas, los conjuntos de predicción obtenidos con este método presentan mayor coherencia clínica, agrupando diagnósticos según su similitud terapéutica y evitando conjuntos redundantes o contradictorios. Como se observó, los conjuntos de predicción ajustados a decisiones reducen la ambigüedad en la interpretación clínica, mejorando la utilidad de los modelos en contextos de alta incertidumbre. Esto permite que los médicos tengan conjuntos de posibles diagnósticos que no solo tienen una garantía estadística de contener la verdad, sino que también son más relevantes y accionables para la planificación del tratamiento.
Estas investigaciones resaltan la importancia de integrar información externa y estructura de decisión en los modelos de inferencia estadística y aprendizaje automático. La robustez ante el sesgo de selección y la adaptación de incertidumbre a la toma de decisiones permiten desarrollar modelos más confiables y útiles en escenarios críticos, desde la formulación de políticas públicas hasta el diagnóstico médico asistido por inteligencia artificial, sentando las bases para sistemas predictivos más justos, interpretables y accionables.
Obtén información sobre Ciencia de datos, Inteligencia Artificial, Machine Learning y más.
Link a la presentación del seminario
https://www.youtube.com/watch?v=8CNPKVwUGtQ&t=3s&ab_channel=QuantilMatem%C3%A1ticasAplicadas
Referencias
En los artículos de Blog, podrás conocer las últimas noticias, publicaciones, estudios y artículos de interés de la actualidad.
