La justicia algorítmica en modelos de aprendizaje se refiere a la aplicación de principios éticos y de equidad en el desarrollo y uso de algoritmos de aprendizaje automático. Estos algoritmos son utilizados para hacer predicciones o tomar decisiones con base en los datos, y pueden tener un impacto significativo en la vida de las personas, por ejemplo, en el ámbito de la selección de candidatos para empleos, la aprobación de préstamos, la evaluación del riesgo de incidir en delitos, entre otros. La justicia algorítmica busca evitar la discriminación y el sesgo en la toma de decisiones basadas en los datos. Sin embargo, existen múltiples definiciones y perspectivas sobre lo que significa la justicia algorítmica y cómo se puede lograr. Estas definiciones pueden ser tan heterogéneas que puede ser imposible obtener dos o más de éstas de forma simultánea en una misma estimación. En este blog, basado en el artículo On Fairness and Calibration [1] se explican dos definiciones distintas de justicia algorítmica y se da una demostración gráfica de la imposibilidad de lograr ambas.
Conceptos de justicia
Se consideran dos definiciones de justicia: Equalized Odds y Calibración. Para esto, se define un clasificador h que toma valores entre 0 y 1, una variable protegida A con dos valores posibles 1 y 2 (por ejemplo, sexo femenino o masculino) y, y como el valor real u observado de la clasificación. Se definen los clasificadores
como las restricciones del clasificador inicial con respecto a los dos posibles valores de A. Además, se definen los valores de generalized false positive rate
y generalized true positive rate 
como:
Con esto es posible definir Equalized Odds: un clasificador satisface Equalized Odds si
Por otro lado, es posible afirmar que un clasificador está perfectamente calibrado si para todo valor 
. Además, satisface el concepto de justicia por calibración si las restricciones del clasificador sobre las categorías de la variable protegida también están perfectamente calibradas. Es decir,
Demostración de imposibilidad
En los artículos On Fairness and Calibration [1] y Inherent trade-offs in the fair determination of risk scores [2] se demuestra la imposibilidad de tener ambas definiciones de justicia algorítmica sobre unos clasificadores . Para esto, se observan inicialmente las implicaciones geométricas de ambos conceptos de justicia.
Dado un clasificador h, es posible representar el rendimiento del modelo en un plano como una tupla
. Si se tienen dos clasificadores con el mismo valor para el generalized false positive rate, significa que los puntos en este espacio deben estar sobre la misma recta vertical como se evidencia en la Figura 1. Por otro lado, si tienen el mismo valor para el generalized true positive rate, entonces los puntos deben estar sobre la misma recta horizontal, como se ve en la Figura 2.
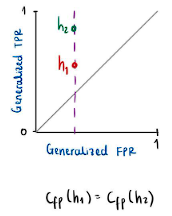
Figura 1
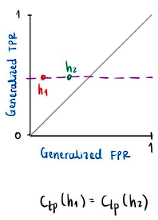
Figura 2
Por lo tanto, para tener Equalized Odds ambos puntos obtenidos deben coincidir, es decir que
Ahora, un clasificador perfectamente calibrado se puede representar con una curva de calibración como la que se muestra en la Figura 3. En esta, se separan las observaciones X en diferentes conjuntos o bins dependiendo de la probabilidad asignada a la observación con el clasificador h. Por ejemplo, si se consideran todas las observaciones a las que se les asignó una probabilidad de 0.1 tenemos que 
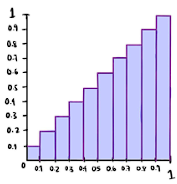
Figura 3
Por la definición de un clasificador perfectamente calibrado se tiene que para cualquier valor p ∈ [0,1]:
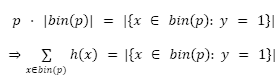
En donde |C| representa la cardinalidad del conjunto C.
Si se utiliza este resultado sobre todos los valores tomados de p
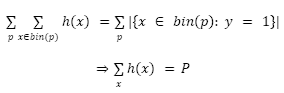
A partir de esto, es posible obtener la siguiente igualdad
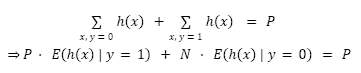
Tomando 
, se tiene que para un clasificador perfectamente calibrado,
es decir que existe una relación lineal entre los valores de 
y de 
. Si ahora se tienen dos clasificadores perfectamente calibrados con valores respectivos de 
, los puntos obtenidos en el plano deben estar en las respectivas rectas definidas por la ecuación obtenida. En la Figura 4 se pueden evidenciar las rectas sobre las cuales se deben encontrar las tuplas para respectivamente.
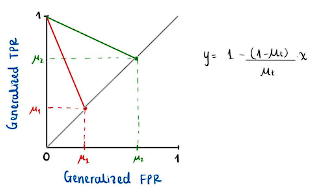
Figura 4
Si además de pedir la calibración de ambos clasificadores, se quiere que estos satisfagan Equalized Odds, los puntos deben coincidir, por lo que deben encontrarse en un punto en el que se intersectan las dos rectas. Si 
entonces el único punto que cumple ambas condiciones es el punto de intersección de ambas rectas, que es la tupla (0,1), la cual representa el clasificador perfecto. Esto concluye la demostración de imposibilidad.
Referencias
[1] G. Pleiss, M. Raghavan, F. Wu, J. Kleinberg, K. Q. Weinberger. On Fairness and Calibration. arXiv:1709.02012, 2017.
[2] J. Kleinberg, S. Mullainathan, and M. Raghavan. Inherent trade-offs in the fair determination of risk scores. In Innovations in Theoretical Computer Science. ACM, 2017.
Obtén información sobre Ciencia de datos, Inteligencia Artificial, Machine Learning y más.
En los artículos de Blog, podrás conocer las últimas noticias, publicaciones, estudios y artículos de interés de la actualidad.
