
En el contexto de los mercados financieros, la optimización de portafolios consiste en identificar la combinación óptima de activos para maximizar la relación retorno-riesgo. No obstante, esta toma de decisiones se realiza en un entorno de incertidumbre, ya que el comportamiento de los activos no es estacionario a lo largo del tiempo. Además, la correlación entre el comportamiento de distintos activos a lo largo del tiempo plantea retos adicionales al intentar determinar cuál es el portafolio óptimo.
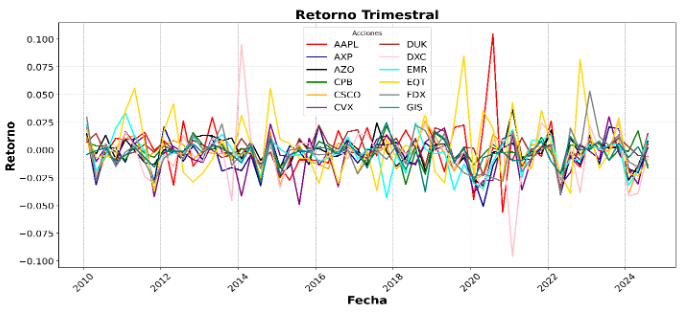
Gráfica 1: Retornos trimestrales de 12 acciones del índice de S&P 500. Se evidencian i) el comportamiento no estacionario de los retornos de los activos y ii) la correlación entre los diferentes retornos de los activos en un mismo momento del tiempo
Los modelos tradicionales como teoría de portafolios de Markowitz y el Modelo de Precios de Activos de Capital (CAPM) han sido ampliamente usados para responder a esta pregunta. No obstante, con el boom del Machine Learning, han surgido una gama de modelos que plantean enfoques alternativos. Uno de ellos es el problema del bandido multiarmado (o Multi-Armed Bandit) y su enfoque con el algoritmo de Thompson Sampling (TS).
Para contextualizar, suponga que usted se encuentra en un casino de Las Vegas y se encuentra frente a 10 jackpots, digamos que cada jackpot es un arma que usted puede disparar, y cada arma tiene una probabilidad de ganar. Su objetivo es maximizar su ganancia o retorno esperado. Existe incertidumbre en el juego, ya que no sabe la probabilidad exacta de ganar, pero puede aproximarse a estas distribuciones utilizando el teorema de Bayes. Al principio, tiene creencias iniciales sobre las probabilidades, pero a medida que avanza, refina su conocimiento en función de los resultados observados.

Gráfica 2: Máquinas Jackpots de casino en Las Vegas
Al inicio del juego, se asume que todas las máquinas tienen la misma probabilidad de ganar. Sin embargo, cada vez que tira de una palanca, obtiene nueva información sobre la probabilidad de ganar. Para decidir qué máquina usar, saca un valor aleatorio de cada distribución y elige la máquina con el valor más alto, lo que permite probar opciones menos exploradas de vez en cuando (exploración), pero enfocándose cada vez más en la mejor opción según los datos obtenidos (explotación). Mediante este trade off entre exploración y explotación, TS logra capturar la noción de retorno versus riesgo para tomar decisiones secuenciales con incertidumbre, aproximándose así a una modelación del comportamiento de los mercados financieros.
Ahora bien, un supuesto importante detrás de TS es que las distribuciones sean estacionarias en el largo plazo, algo que no se cumple en el caso de los portafolios financieros. Por ello, han surgido extensiones de TS para flexibilizar este supuesto. Los algoritmos de Adaptive Thompson Sampling (ADTS) y Combinatorial Adaptive Thompson Sampling (CADTS), propuestos por Fonseca, Silva y Castro en 2024, descomponen el comportamiento de los portafolios en componentes de largo y corto plazo. Estos algoritmos incorporan un parámetro de corto plazo que depende de una ventana temporal preestablecida. Así, las decisiones sobre el portafolio que maximiza los retornos en cada periodo se basan en una ponderación entre el parámetro de largo plazo y el de corto plazo.
Esta hipótesis no es descabellada en el mundo real. Por ejemplo, considere el caso de Apple, que es una empresa consolidada y fuerte en el mercado. Sin embargo, a principios de 2024, el lanzamiento de su producto Apple Vision Pro resultó en ventas limitada, situación que afectó negativamente a la compañía. Un caso similar es el de Tropicana, propiedad de PepsiCo. En 2009, la marca rediseñó su logo, pero los clientes no reconocieron el nuevo diseño, lo que llevó a una disminución significativa en las ventas y, finalmente, a la decisión de volver al logo antiguo.
Por otro lado, volviendo al problema de la correlación entre los retornos de los portafolios, una propuesta interesante es combinar ADTS con el proceso de ortogonalización por PCA propuesto por Ozkaya y Wang en 2020. Este proceso de ortogonalización se aplicaría antes de ADTS para reducir la dimensionalidad del problema, disminuyendo el número de portafolios y garantizando que sean independientes entre sí, de manera que contengan únicamente la información relevante.
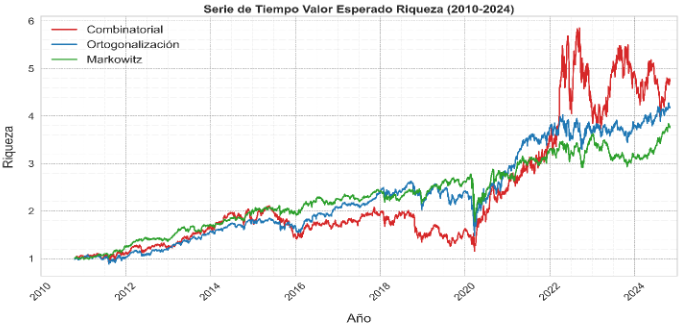
Gráfica 3: Riqueza esperada de invertir un dólar al inicio del período
En la Gráfica 3 se muestra una comparación del rendimiento de la metodología de ortogonalización con ADTS (en azul), CADTS (en rojo) y la metodología tradicional de Markowitz (en verde), suponiendo que se invirtió un dólar al inicio del periodo. Los resultados indican que CADTS es bastante volátil, aunque al final del periodo (2022-2024) muestra un rendimiento superior al de los otros algoritmos. Esta volatilidad podría deberse a un golpe de suerte, dado que en las simulaciones solo se incorporó la maximización del retorno esperado. Por otro lado, a pesar de que el modelo de ortogonalización con ADTS también se basa solo en el retorno, la ortogonalización hace que el comportamiento sea más moderado al reducir el conjunto de opciones. Finalmente, el algoritmo tradicional de Markowitz presenta un rendimiento más prudente a lo largo del tiempo (2011-2024), ya que no solo incorpora la noción de retorno, sino también la de riesgo, lo que genera decisiones más conservadoras. Para concluir, los métodos de Multi-Armed Bandits parecen ser prometedores. En el futuro, la tarea será explorar su potencial, especialmente incorporando de manera explícita nociones de riesgo como con el Sharpe ratio.
Obtén información sobre Ciencia de datos, Inteligencia Artificial, Machine Learning y más.
Link a la presentación del seminario
https://www.youtube.com/watch?v=OKwBVOxwBBw
Referencias
Ozkaya, G., & Wang, Y. (2023). Multi-Armed Bandit Approach to Portfolio Choice Problem. Barcelona Graduate School of Economics.
Fonseca, G., Silva, L., & Castro, P. (2024). Improving Portfolio Optimization Results with Bandit Networks.
Fama, E. F., & French, K. R. (1993). Common Risk Factors in the Returns on Stocks and Bonds. Journal of Financial Economics, 33(1), 3–56.
En los artículos de Blog, podrás conocer las últimas noticias, publicaciones, estudios y artículos de interés de la actualidad.